L’entropie, ou pourquoi les Incubators essaient de nous encuber à sec
Nous sommes les 21 décembre, soit à deux jours de la fin des quartiers libres d’hivers. Et aussi le jour de la fin du monde, mais c’est un détail (ouais, je sais, tout le monde la fait et c’est chiant, mais je ne pouvais pas mentionner la date sans le dire, donc comme ça, c’est fait, et on en parle plus). Pour toutes ces raisons, j’ai pensé que ça serait un bon jour pour enfin faire l’article que je pense écrire depuis le début du quartier libre. Alors cessons ce teasing et allons y !
Si vous avez suivi le quartier libre de printemps qui s’est tenu ici, vous avez déjà pu lire un de mes articles. Comme vous avez pu le deviner grâce au titre, cet article sera encore un tentative de lier un anime avec une petite explication scientifique pour nous aider à comprendre un phénomène. Mais cette fois, plus qu’une faute sur un fichier de traduction pas vraiment très légal, c’est une critique qui s’est répandue à travers le web que je vais essayer de démonter.
Donc oui, l’article d’aujourd’hui sera à propos de la série Puella Magi Madoka Magica. C’est pas que je suis fan de cet anime, Madoka est juste devenue ma déesse, mais j’avais quand même envie de contrer ces conneries que je vois fleurir à travers le web à propos de la soit disant contradiction qu’on aurait entre l’entropie et le voyage temporel. Cet article contient du léger spoil de l’anime, donc si vous ne l’avez pas vu et que vous voulez vraiment vous gardé de la moindre révélation dessus, je vous déconseille de le lire. Enfin,un peu comme pour l’article de Raton. Voilà, si vous continuez à lire et êtes spoilés, ne venait pas vous plaindre. Vous avez été prévenu. Nous pouvons donc commencer !
Rapide tour de l’origine de la mésentente
L’entropie, je suis sûr que vous en avez tous déjà entendu parlé. Mais si, vous savez, cette chose que votre prof de physique évoquait sur un coin table en ayant pas vraiment l’air sûr de lui. Ou bien ce truc dont vous a parlé un membre de votre famille (ou un ami, ne soyons pas mauvaise langue) lors d’une soirée bien arrosée, mais qui ne semblait pas comprendre bien ce que c’était non plus. Mais il y a quand même une chose que l’on sait tous, c’est que l’entropie est mesure le désordre d’un système. Mais qu’est-ce que ça veut dire exactement ? Déjà, c’est quoi, le désordre ? Ça a une définition mathématique ? Et puis, j’ai pu lire quelque chose sur le web… C’était quoi déjà ? Ah oui, que l’entropie augmente toujours au cours du temps. Mais pourquoi le désordre augmente toujours autour du temps ? Ça veut dire que si je ferme une pièce à clef et que je reviens des années plus tard, tous les objets se seront déplacés tous seuls ? Bah, c’est pas trop important, j’ai à peu près compris, je suis pas physicien, c’est pas mon boulot, hein.
Voici donc à peu près, de ce que j’ai pu voir, où s’arrête la compréhension de l’entropie de beaucoup de personne (dont certains étudiants en physique, ce qui est un peu plus inquiétant, mais le degré d’analyse des étudiants du supérieur n’est pas le sujet de cet article). Ce n’est pas un problème, en soit. C’est pas comme si on allait vous demander de calculer l’entropie d’un système demain à votre boulot, non plus. Ça offre une petite vision d’ensemble de la chose, ce qui est largement suffisant pour avoir une petite idée du monde qui nous entoure.
Là où ça devient beaucoup plus gênant, c’est quand des gens se servent de cette connaissance partielle pour essayer d’argumenter un problème dans le blabla scientifique d’un anime. Et manque leur cible d’un bon kilomètre. Oui, le blabla scientifique de Madoka manque tout de même clairement de rigueur, mais bon, je ne demande à trouver un cours de physique dans mes animes non plus. Mais voyons avant tout de même quelle est leur thèse.
Elle tient en fait en quelques phrases. Les Incubators cherchent à contrer l’entropie. Pour cela, ils collectent l’énergie engendrer par des jeunes filles en fleur, en se servant d’une partie de cette énergie pour exaucer leur vœu le plus cher. Le vœu de Homura lui permet de manipuler de le temps, et même de le remonter, quand la date le permet. L’entropie croît forcément au cours du temps. Donc les Incubator ont trouvé une manière de contrer l’entropie pour permettre à le fille aux cheveux noir de remonter le temps.
NAN ! STOP ! VOUS AVEZ TORT ! C’EST FAUX ! STOP, STOP, STOP !
Bon, dit comme ça, ça semble logique. Mais cela vient de la connaissance partielle que nous avons jusqu’à présent de l’entropie. Voyons donc un peu plus précisément ce que c’est.
L’entropie, quoi que c’est que ce truc?
En premier lieu, avant de rentrer dans le vif du sujet, j’aimerais définir un concept simple en physique, mais assez fondamental pour mieux saisir l’ensemble de ce que je vais dire ensuite. C’est le concept de système. Dans cette science, on parle souvent de système étudié. Cela désigne tout simplement l’objet que l’on étudie. Ça peut être un échantillon de gaz, une bille, un cristal, tout comme une planète, une galaxie entière ou même vous. Voilà, comme ça on est clair sur les termes.
On peut donc commencer. Avant toute chose, oublions la définition courante de l’entropie. Le désordre, c’est bien beau, mais la rigueur derrière ce terme laisse un à désirer. Nous allons donc la définir comme « une mesure du nombre de configurations que peut prendre le système ». Je sens que j’ai déjà filé des maux de tête à la moitié du lectorat en écrivant cette phrase. Je vais prendre exemple pour vous l’expliquer un peu mieux. Vous avez une boîte avec trois compartiments. Vous avez deux balles à mettre dedans. On va dire que les deux balles sont totalement identiques, donc on s’en fiche si vous mettez la balle 1 dans le compartiment 1 et la balle 2 dans le compartiment 2 ou l’inverse. Vous avez alors trois possibilités pour placer vos balles :
- Une dans le compartiment 1, une dans le compartiment 2
- Une dans le compartiment 1, une dans le compartiment 3
- Une dans le compartiment 2, une dans le compartiment 3
Voilà, vous avez dénombré le nombre de configuration que pouvez prendre votre système. C’est 3. Pour la suite, on va noter pour le moment ce chiffre n. Vous pouvez maintenant facilement trouver l’entropie de votre système grâce à cette simple formule :
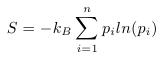
Bon, on va attendre que les évanouis se réveillent avant de passer aux explications.
…
On va dire que c’est bon, vous expliquerez le reste aux autres. Décortiquons donc un peu cette formule.
- S représente l’entropie. Me demandez pas pourquoi cette lettre, j’en sais rien, c’est historiquement comme ça. Si vous voulez vraiment savoir, inventez une machine à remonter (ah bah tiens, on y revient) le temps et aller demander ça aux scientifiques de la fin de XIXéme.
- Le kB est la constante de Boltzmann. En gros, elle nous permet de normaliser la formule et de la mettre dans les bonnes unités. Autrement dit, dans le cadre de cette explication rapide, on s’en fout.
- Σ (sigma) est le signe symbolisant la somme. Ici, on indique par l’indice « i » que c’est cette variable qui va augmenter, de 1 en 1, de 1 jusqu’à n. On va donc faire p1lnp1 + p2lnp2 + p3lnp3 + … + pnlnpn
- pi représente la probabilité du système d’être dans l’état i (on nomme ici les états par des numéros). Par exemple, on peut prendre :
- l’état 1, une balle dans le compartiment 1, une balle dans le compartiment 2, qui a 40 % de chance d’exister (p1 = 0,4)
- l’état 2, une balle dans le compartiment 1, une balle dans le compartiment 3, qui a 30 % de chance d’exister (p2 = 0,3)
- l’état 3, une balle dans le compartiment 2, une balle dans le compartiment 3, qui a 30 % de chance d’exister (p3 = 0,3)
( p1, p2 et p3 sont toutes les possibilités de configuration du système, on doit donc avoir p1 + p2 + p3 = 1, ce qui traduit le fait que le système est forcément dans une de ces configurations)
On pourra alors calculer l’entropie du système :

Félicitation, vous avez trouvé votre première valeur d’entropie. En physique, ce résultat représente par exemple l’entropie d’une molécule composée de trois atomes figés.
Bon, voilà, maintenant, vous avez à peu près compris ce que voulais dire cette équation. Mais ensuite ? C’est quoi le rapport avec le nombre de configurations qu’on a vu tout à l’heure ? Et bien, comme vous pouvez le voir, la somme que l’on fait va au maximum à i = n, soit le nombre de configurations de notre système. Pour faire rapide, plus n sera grand, plus on aura de termes dans la somme, et donc plus S sera grand. Σpilnpi représente donc les configurations de notre système. D’ailleurs, quand le système qu’on étudie n’interagit d’aucune façon avec l’extérieur (c’est expérimentalement impossible, c’est un cas d’école), la formule devient :
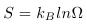
où Ω représente le nombre de configuration de notre système (si vous voulez tenter avec le système que j’ai donné, ça ne marchera pas : un système isolé a toute ses probabilités égales entre elles. Ici, il faudra prendre p1 = p2 = p3 = 1/3).
Voilà, vous savez techniquement tout ce que vous avez besoin de savoir de l’entropie. En fait, à partir de là, vous pouvez en déduire même la plupart des théories scientifiques qui viennent de l’entropie, soit à peu près toute la physique statistique classique. Mais cela vous prendrait un peu de temps, donc on va éviter de le faire ici. On va s’arrêter à une étude simple.
Une étude simple de la légende urbaine
Comme on vient de le voir, l’entropie dépend uniquement des configurations que peut prendre le système. En aucun cas le temps n’entre en compte dans sa formule. Ni aucune dérivée par rapport à celui-ci.
Cependant, il y a deux grandeurs qui rentre en compte implicitement dans ces formules : le volume et la température. Pour le volume, cela se comprend assez simplement. Par exemple, prenons un ballon avec n atomes d’oxygène dedans. Si on augmente la taille du ballon sans augmenter la quantité d’oxygène (par exemple en faisant diminuer la pression en dehors du ballon), les atomes auront plus de place et pourront donc prendre plus de positions différentes. Il y aura donc plus de configurations possibles, et l’entropie augmentera. Au contraire, si on compresse le ballon avec ses mains, on fait diminuer le volume du ballon, les atomes ont donc moins de positions disponibles, donc il y a moins de configurations possibles, donc l’entropie diminue. Oui, vous avez bien lu, on peut faire diminuer l’entropie au cours du temps, suffit de serrer un ballon dans ses mains. Attention tout de même, pour que cela marche avec l’entropie, il faut que le ballon n’interagisse en aucun cas avec l’extérieur autrement que via la force exercée par la pression ou vos mains (pas d’échange de chaleur, ni de quantité de matière). Mais vous allez voir, c’est encore plus drôle avec la température.
La dépendance en température est plus dur à voir. Pour faire rapide, la température représente une énergie qu’ont les particules qui composent le matériau. Logiquement, quand cette énergie est élevé, les particules peuvent se déplacer plus facilement. D’ailleurs, c’est pour ça que, quand il fait trop chaud, les matériaux fondent : les particules qui les constituent ont acquis assez d’énergie par la chaleur pour briser les liaisons entre elles et elles peuvent donc se déplacer plus librement ; le solide devient alors liquide. Si on chauffe plus, elles gagnent encore d’énergie, et il arrivera un moment où les liaisons entre les molécules disparaîtront complètement et le liquide deviendra un gaz. Ces passages de solide à liquide et de liquide à gaz sont appelés transitions de phase (il en existe d’autres, mais il est totalement inutile d’en parler ici, si vous voulez savoir, vous pouvez toujours me demander ou aller interroger wikipedia).
Vous l’aurez compris, si la température augmente, les molécules ont plus d’énergie disponible et peuvent donc se déplacer plus librement. Elles peuvent atteindre de nouvelles positions, il y a donc plus de configurations possibles. Et l’entropie augmente. Par exemple, quand vous mettez votre poulet au four, vous faites augmenter son entropie. Et, plus drôle, quand vous mettez de l’eau au congélateur, vous faites diminuer son entropie. Vous la faites même diminuer suffisamment pour induire une transition de phase liquide-solide. Oh, encore une diminution d’entropie dans la vie de tous les jours.
Je peux vous garantir que, que ce soit pour le ballon que vous serrez ou pour vos glaçons dans le congélateur, ils n’ont pas remonté le temps. D’où vient du coup cette idée que l’entropie augmente forcément au cours du temps ? Il y a bien une raison. Le volume de l’univers augmente en permanence. Il n’y a pas de matière créée en son sein. Il n’échange ni de matière ni d’énergie avec l’extérieur. L’entropie de l’univers augmente donc obligatoirement avec le temps.
Bon, là, maintenant, les personnes qui se sont un peu renseignée me sortiront la seconde loi de la thermodynamique. Temps de passer à une petite explication.
La seconde loi de la thermodynamique
« L’entropie d’un système isolé ne décroît jamais, ce type de système évolue toujours spontanément vers l’équilibre, soit l’état de plus haute entropie. »
Voilà ce que nous dit la thermodynamique. Un système isolé isolé est un système qui n’interagit pas avec l’extérieur. Exactement comme notre ballon tout à l’heure si on enlève la pression de vos mains. Ou l’univers. En gros, on est sur une redite de ce que j’ai tout à l’heure.
Ce principe induit qu’on ne peut pas revenir à état qu’on a précédemment occupé. Un état est un ensemble des valeurs caractérisant un objet, dont l’entropie fait partie. C’est le principe irréversibilité. Dans un système irréversible (sauf quelques rares cas, à peu près tous les systèmes physiques évoluant dans le temps sont irréversibles), si on est passé par un état X à un instant t0, il est impossible que l’on revienne exactement à cet état X à un instant t0 + a, a un nombre quelconque. Remarquez bien que j’ai bien noté t0 + a. Autrement dit, si on place à un instant t0 + a quelconque, qu’on trouve le moyen de remonter le temps de a pour revenir à l’instant t0, on retombera exactement l’état X, avec exactement la même valeur d’énergie. Tout ce que nous dit le second principe de la thermodynamique, c’est que pour t croissant, S sera croissant.
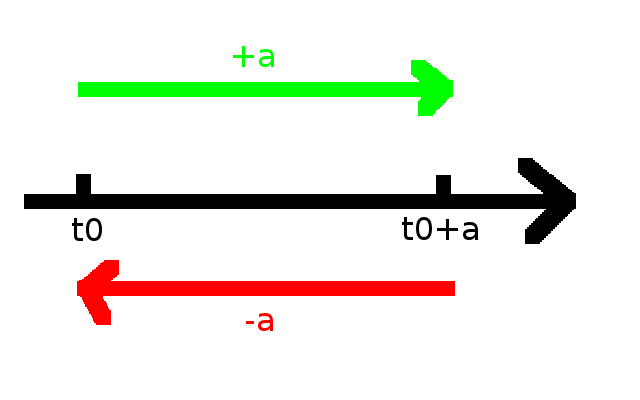
C’est tout. Point barre. Rien d’autre.
Et si jamais vous n’êtes pas convaincu, je ferais simplement une dernière remarque. La relativité d’Einstein (restreinte ou générale, ça marche pour les deux) prévoit la possibilité de voyager dans le temps si on va plus vite que la vitesse de la lumière (même si c’est techniquement impossible pour des humains, il y a des physiciens théoriciens qui ont supposés l’existence de particule pouvant remonter le temps ainsi). Ces théories sont totalement compatibles avec la physique statistique classique, qui repose entièrement sur l’entropie. Vous voulez vraiment contredire un siècle de physique ?
Mais alors, pourquoi les Incubators essaient de nous enculer à sec?
Bon, c’est pas tout ça, mais ça va faire quatre pages que je blablate de physique, d’entropie, tout ça, mais ça parle quand même pas beaucoup d’anime, cet article. Voyons un peu ce que pourrais vouloir faire les Incubators.
Ils veulent donc empêcher l’entropie de croître indéfiniment. Là, comme ça, à quatre heures du mat’, je verrais à peu près trois solutions. Vous êtes libre d’en proposer aussi de votre côté, si vous avez des idées, je ne suis pas forcément très fort pour ça.
La première consisterais à contrer l’expansion de l’univers. Donc contrer ce que les scientifiques nomment l’énergie noire, une énergie dont on ne sait pas grand chose si ce n’est qu’elle contre la force de gravitation de toute la matière comprise dans l’univers pour forcer son expansion à se continuer. La contrer pourrait revenir à placer une masse immense quelque part dans l’univers pour créer une force d’attraction suffisante pour retenir cette expansion. Comme ça, je n’ai pas vraiment de l’ordre de grandeur de cette masse, si ce n’est qu’elle n’aurait pas d’équivalent dans l’univers, je pense… Et il y a pas mal de chances pour que toute la matière finisse pas être attirée par cette masse gigantesque.
La seconde solution serait de mettre proche de l’univers une source extrêmement froide qui pomperait sa chaleur. Actuellement, la température de l’univers, si on se place loin de toute source d’énergie est de 2,728 K (- 270,424°C). Quand il atteindra 0K, tout sera figé, car il n’y aura plus assez d’énergie pour que ne serait-ce qu’un ne quark bouge.
Enfin, on pourrait changer le point d’équilibre de l’univers pour que ça soit l’actuel. Mais une fois l’équilibre atteint, un système physique ne bouge plus. Atteindre l’équilibre voudrait donc dire, à nouveau, atterrir dans un univers figé.
C’est pas très gai tout ça, quand même. Finalement, ça vaut vraiment le coup de vouloir arrêter l’entropie ? C’est pas même antinomique de la vie ? La vie, c’est croître, faire des choses, changer, agir, bouger… Une entropie qui ne bougerait, ça voudrait dire arrêter tout, un figement définitif, à moins d’avoir une force d’énergie suffisante pour faire considérablement bouger l’univers de sa position d’équilibre et le remettre en marche. Une énergie qui ne pourra, par définition, pas se trouver dans l’univers, puisque celui-ci sera figé. Vraiment pas encourageant, hein ?
Voilà tout. Merci de m’avoir lu jusque là, si vous avez tenu. Félicitation pour votre courage, et merci de votre intérêt. J’espère que vous avez à peu près pu me suivre durant tout mon blabla, et que vous aurez pu comprendre ce que je voulais dire. Je suis désolé du peu d’image, particulièrement de Madoka, que j’ai mis dans cet article, mais il ne s’y prêtait pas non plus vraiment. Ça faisait un moment que je voulais le faire, qu’il me trottait dans la tête, et ça du bien de l’avoir enfin coucher sur bits (je ne peux honnêtement pas dire que je l’ai couché sur papier). J’espère qu’il vous aura plus, et qu’on se retrouvera au prochain Quartier Libre, si j’ai de nouvelles idées d’ici là. Peut-être que si jamais je trouve des informations sur Utsuo Reiuji, je pourrais vous faire un cours sur la fusion nucléaire ?

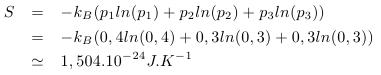

14 commentaires